Solving Median String Problem in DNA using MapReduce

Genomes are fascinating. They are the sole source of information in living beings. Computational genetics, biochemistry and biology are rife with problems that are np-hard. As computer scientists, our goal is to come up with solutions that solve the problem biologists are facing in a way that is time and memory efficient.

Prologue: The Median String Algorithm and Motifs

So, what exactly are motifs? Before answering the question, let’s look how gene sequences look like. Wikipedia states that, “A nucleic acid sequence is a succession of letters that indicate the order of nucleotides forming alleles within a DNA (using GACT) or RNA (GACU) molecule. By convention, sequences are usually presented from the 5’ end to the 3’ end. For DNA, the sense strand is used. Because nucleic acids are normally linear (unbranched) polymers, specifying the sequence is equivalent to defining the covalent structure of the entire molecule. For this reason, the nucleic acid sequence is also termed the primary structure.”
A gene sequence looks as shown below:

ACAAGATGCCATTGTCCCCCGGCCTCCTGCTGCTGCTGCTCTCCGGGGCCACGGCCACCGCTGCCCTGCC
CCTGGAGGGTGGCCCCACCGGCCGAGACAGCGAGCATATGCAGGAAGCGGCAGGAATAAGGAAAAGCAGC
CTCCTGACTTTCCTCGCTTGGTGGTTTGAGTGGACCTCCCAGGCCAGTGCCGGGCCCCTCATAGGAGAGG
AAGCTCGGGAGGTGGCCAGGCGGCAGGAAGGCGCACCCCCCCAGCAATCCGCGCGCCGGGACAGAATGCC
CTGCAGGAACTTCTTCTGGAAGACCTTCTCCTCCTGCAAATAAAACCTCACCCATGAATGCTCACGCAAG
TTTAATTACAGACCTGAA

The letters A, C, G and T are representative of the Nucleotides.

Motifs Definition

In genetics, a sequence motif is a nucleotide or amino-acid sequence pattern that is widespread and has, or is conjectured to have, a biological significance. For proteins, a sequence motif is distinguished from a structural motif, a motif formed by the three-dimensional arrangement of amino acids which may not be adjacent. Obviously, there can be mutations in the motif and the consensus motif can be different from the actual motif pattern in the DNA sequence.

How to find motifs?

Say, we have a long DNA sequence, how should we go about finding the consensus motif? Obviously, we have to have a predefined length for the motif. This is also called L-mer. For example, if you take target motif sequences of length 8, the target is to find 8-mer. Median String algorithm is one of the algorithms to find consensus motif. The algorithm is presented as follows:

Few Terms before we start the actual algorithm

$t$: Number of sample DNA sequences

$n$: Length of each DNA sequence

$DNA$: Sample of DNA sequences $t \times n$ array

$l$: length of the motif $ l - $ mer

$s_i$: Starting position of an $ l- $ mer

$s = (s_1, s_2, …, s_t) $: array of motif’s starting positions

An example is shown in the figure below:

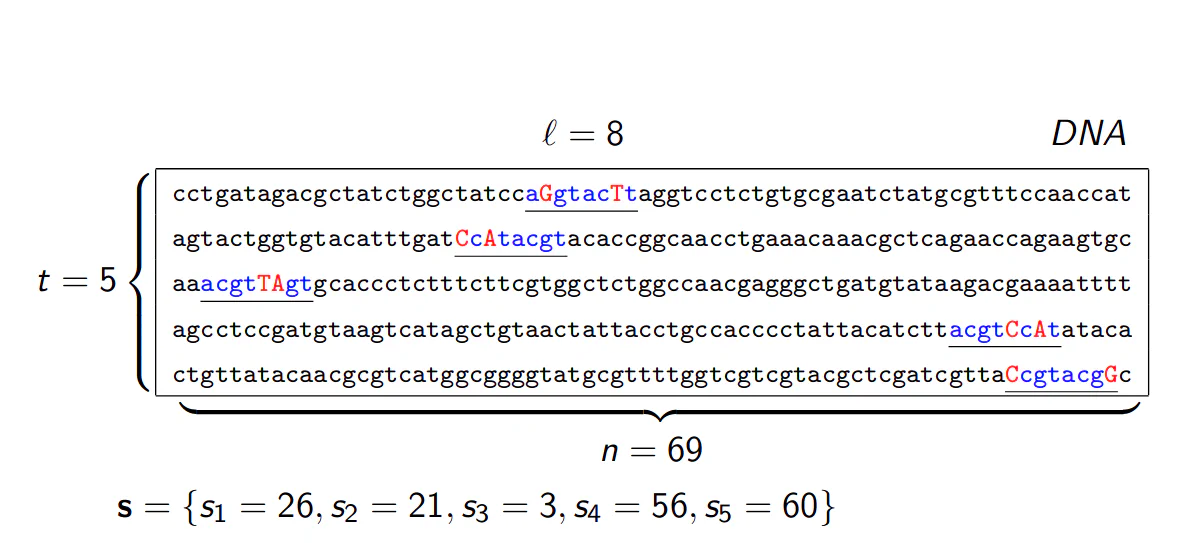
Scoring Motifs

Given, $$s = (s_1, s_2, …, s_t) $$ and $$ DNA $$:

Here, $$ \text{count}(c, j) $$ gives the number of times that symbol c equals $$ DNA[i][s_i + j - 1] $$

The Median String Problem

The median string problem is formulated as:

• Given a set of $$ t $$ $$DNA$$ sequences find a pattern that appears in all t sequences with the minimum number of mutations.
• This pattern will be motif

Transgression: Hamming Distance

• The Hamming Distance $$ d_H(v, w) $$ is the number of nucleotide pairs that do not match when v and w are aligned
• For example $$ d_H(AAAAAA, ACAAAC) = 2 $$

Transgression: Total Distance

• For each $$ DNA $$ sequence $$ i $$, calculate all $$ d_H(v, x) $$, where $$ x $$ is an $$ l-mer $$ with starting position $$ s_i ( 1 \leq s_i \leq n-l+1) $$
• Find minimum of $$ d_H(v, x) $$ among all $$ l-mers $$ is sequence $$ i $$
• $$ \text{TotalDistance} (v, DNA) $$ is the sum of minimum Hamming distance for each $$DNA$$ sequence $$ i $$.

The total distance is shown in the example below:

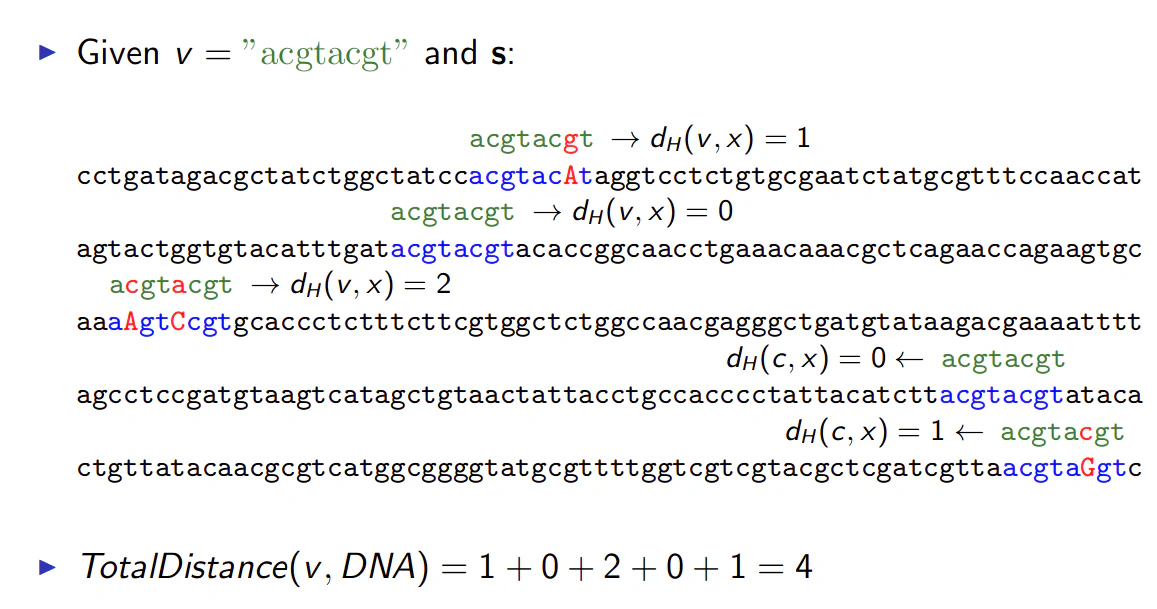
Formulating the Median String Problem

The median string problem is formulated as:

• Goal: Given a set of DNA sequences, find a median string
• Input: a $$ t \times n $$ matrix $$DNA$$, and $$l$$, the length of the pattern to find
• Output: A string $$ v $$ of $$ l $$ nucleotides that minimizes $$ TotalDistance(v, DNA) $$ over all strings of that length

The algorithm is shown below:

$$ MedianStringSearch(DNA, t, n, l): $$

1: $ bestWord \longleftarrow AAA…A $

2: $ bestDistance \longleftarrow \infty $

3: $ \mathbf{for} $ each $l-mer$ $v$ from $AAA…A$ to $TTT…T$ $\mathbf{do}$:

4:      $ \mathbf{if} $ $ TotalDistance(v, DNA) < bestDistance $ $ \mathbf{then}$:

5:           $ bestDistance \longleftarrow TotalDistance(v, DNA) $

6:           $ bestWord \longleftarrow TotalDistance(v, DNA) $

7: $ \mathbf{return }$ $ bestWord $

How to use MapReduce and Hadoop to solve this problem?

Now, consider the median string algorithm to find $ 8-mer $$. The total number of candidate target motifs from $$AAAAAAAA$$ to $$TTTTTTTT$$ is $$4^8$$. Let us convert the algorithm into hadoop map-reduce problem, as shown in the figure below:

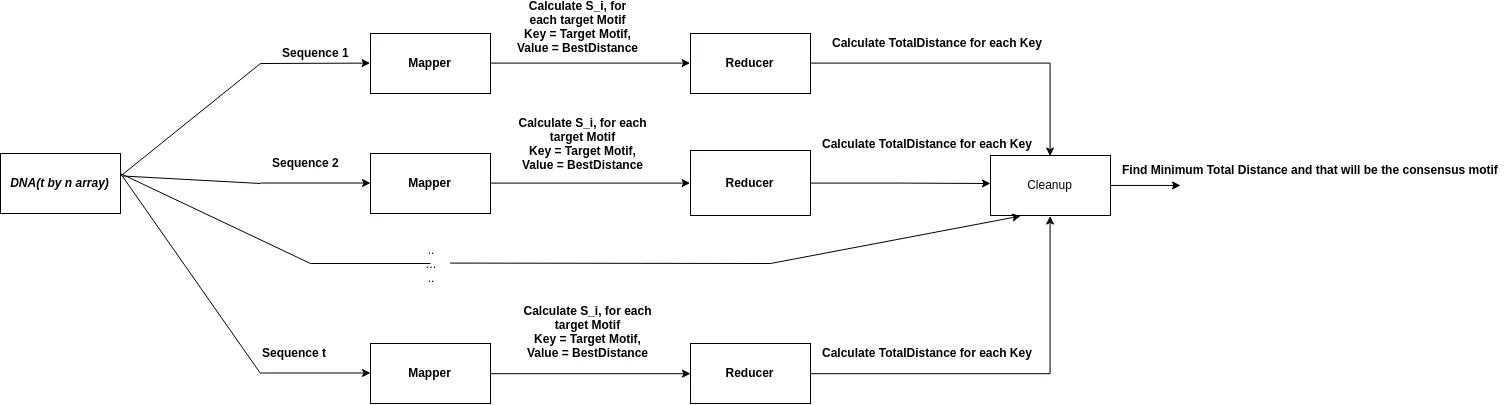
If you have a long DNA array spread over many lines and multiple text files, first thing you need to focus on is the way to parallelize the algorithm. One way to implement the algorithm with Hadoop is to do this:

1. For every DNA sequence line, calculate the best distance and start indexes for every target motif between AAAAAAAA to TTTTTTTT. This function should be implemented in the mapper class of Hadoop. Hadoop uses a <key, value> for the map operation output. Think of the target motif as the key and there will be multiple values for each key will be the best distance for each DNA seqeunce line.
2. The reducer takes in the <key, values> : (targetmotif, bestDistancesForEachSequence) produced by the mapper and calculates the distanceScore for each key like this:For each value of values: distanceScore += value
3. In the reducer class, save the distanceScore for each key. After the reduce operation is complete, call on the cleanup function to find the minimum distanceScore. The key for the distance score will be the consensus motif.
4. If we need more information than just the best distance from the final output, we have to customize the Output class of Mapper and write our own custom implementation that either implements the Writable or WritableComparable interface. For example, if you want to send the sequenceId(line number), together with the best distance for each target motif from the mapper, you have to write your own class.

Epilogue: Enough Already. Where’s the implementation?

In couple of days, I will be posting a link to a github repository that has the solution. I will be also posting instructions on how to run the code in Amazon EMR.